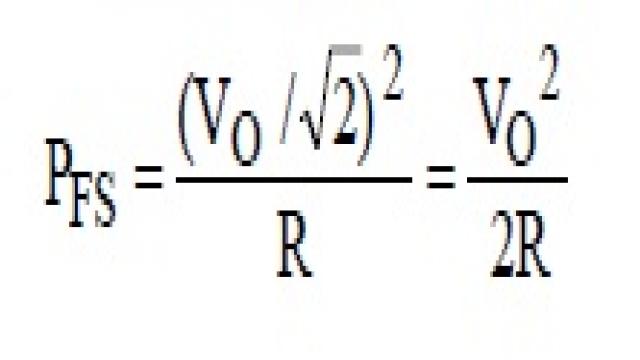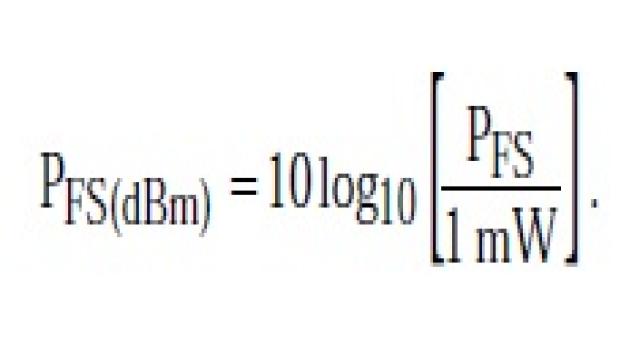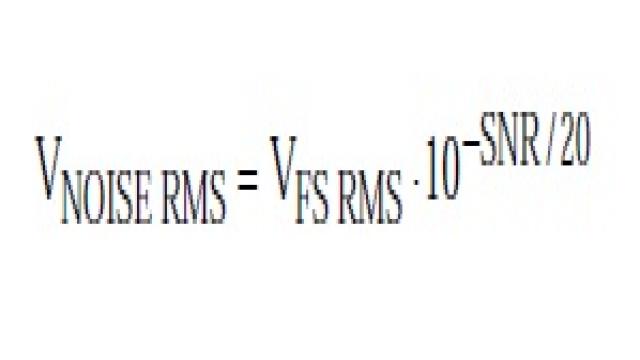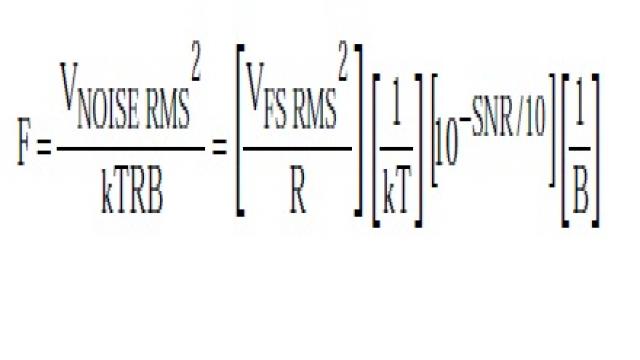噪聲系數(NF)是RF系統設計師常用的一個參數，它用于表征RF放大器、混頻器等器件的噪聲，并且被廣泛用作無線電接收機設計的一個工具。許多優秀的通信和接收機設計教材都對噪聲系數進行了詳細的說明，本文重點討論該參數在數據轉換器中的應用。

現在，RF應用中會用到許多寬帶運算放大器和ADC，這些器件的噪聲系數因而變得重要起來。參考文獻2討論了確定運算放大器噪聲系數的適用方法。我們不僅必須知道運算放大器的電壓和電流噪聲，而且應當知道確切的電路條件：閉環增益、增益設置電阻值、源電阻、帶寬等。計算ADC的噪聲系數則更具挑戰性，大家很快就會明白此言不傳。

當RF工程師首次計算哪怕是最好的低噪聲高速ADC的噪聲系數時，結果也可能相對高于典型RF增益模塊、低噪聲放大器等器件的噪聲系數。為了正確解讀結果，需要了解ADC在信號鏈中的位置。因此，當處理ADC的噪聲系數時，務必小心謹慎。

ADC噪聲系數定義

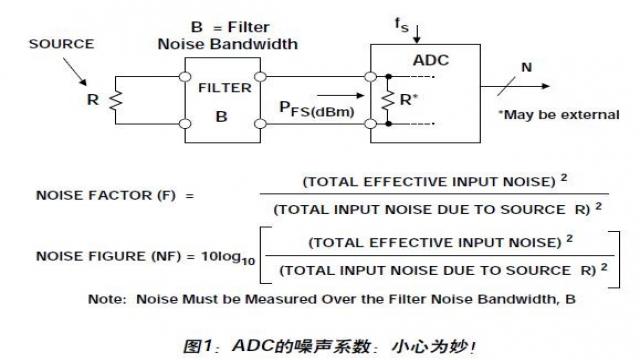
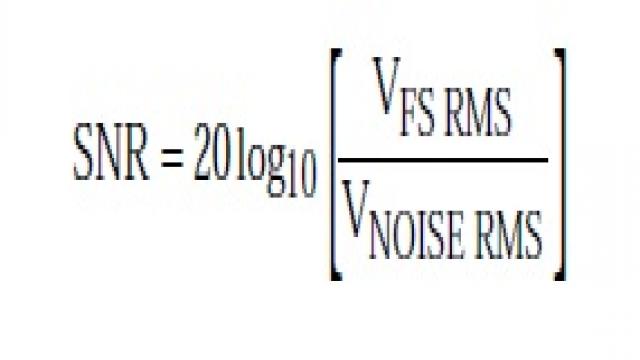
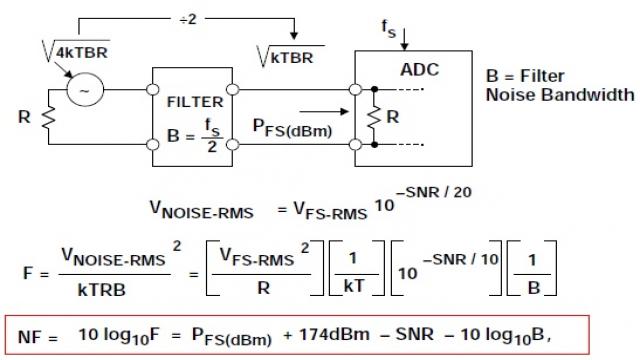
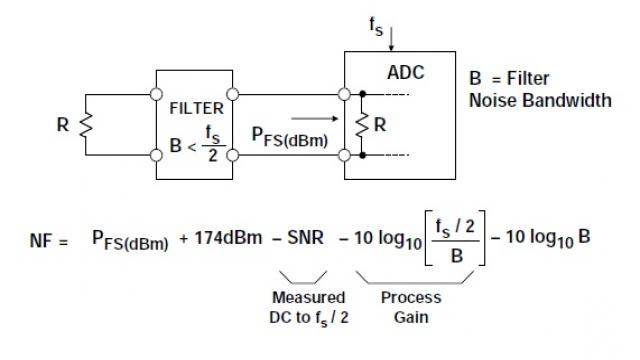
圖1顯示了用于定義ADC噪聲系數的基本模型。噪聲因數F指的是ADC的總有效輸入噪聲功率與源電阻單獨引起的噪聲功率之比。由于阻抗匹配，因此可以用電壓噪聲的平方來代替噪聲功率。噪聲系數NF是用dB表示的噪聲因數，NF = 10log10F。

該模型假設ADC的輸入來自一個電阻為R的信號源，輸入帶寬以fs/2為限，輸入端有一個噪聲帶寬為fs/2的濾波器。還可以進一步限制輸入信號的帶寬，產生過采樣和處理增益，稍后將討論這種情況。

該模型還假設ADC的輸入阻抗等于源電阻。許多ADC具有高輸入阻抗，因此該端接電阻可能位于ADC外部，或者與內部電阻并聯使用，產生值為R的等效端接電阻。

ADC噪聲系數推導過程

滿量程輸入功率是指峰峰值幅度恰好填滿ADC輸入范圍的正弦波的功率。下式給出的滿量程輸入正弦波具有2VO的峰峰值幅度，對應于ADC的峰峰值輸入范圍：

v(t) = Vosin2πft                                    等式1

該正弦波的滿量程功率為：

等式2
通常將此功率表示為dBm（以1 mW為基準）：

等式3

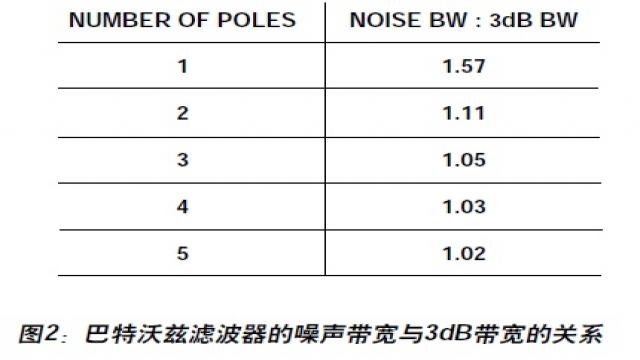
對濾波器的噪聲帶寬B需要加以進一步的討論。非理想磚墻濾波器的噪聲帶寬指的是讓相同的噪聲功率通過時，理想磚墻濾波器所需的帶寬。因此，一個濾波器的噪聲帶寬始終大于其3dB帶寬，二者之比取決于濾波器截止區的銳度。圖2顯示了最多5極點的巴特沃茲濾波器的噪聲帶寬與3dB帶寬的關系。注意：對于2極點，噪聲帶寬與3dB帶寬相差11%；超過2極點后，二者基本相等。

NF計算的第一步是根據ADC的SNR計算其有效輸入噪聲。ADC數據手冊給出了不同輸入頻率下的SNR，確保使用與目標IF輸入頻率相對應的值。此外還應確保SNR數值中不包括基波信號的諧波，有些ADC數據手冊可能將SINAD與SNR混為一談。知道SNR后，就可以從下式開始計算等效輸入均方根電壓噪聲：

等式4

求解得：

等式5

這是在整個奈奎斯特帶寬(DC至fs/2)測得的總有效輸入均方根噪聲電壓，注意該噪聲包括

源電阻的噪聲。

下一步是實際計算噪聲系數。在圖3中，注意源電阻引起的輸入電壓噪聲量等于源電阻

sqrt(4kTBR)的電壓噪聲除以2，即sqrt(kTBR)，這是因為ADC輸入端接電阻形成了一個2:1衰減器。

噪聲因數F的表達式可以寫為：

等式6

將F轉化為dB并簡化便可得到噪聲系數：

NF = 10log10F = PFS(dBm) + 174 dBm – SNR – 10log10B,等式7

其中，SNR的單位為dB，B的單位為Hz，T = 300 K，k = 1.38 × 10–23 J/K。

圖3：根據SNR、采樣速率和輸入功率求得的ADC噪聲系數

其中SNR的單位是dB,帶寬B是Hz,T=300K,k=1.38 × 10–23 J/K

過采樣和數字濾波會產生處理增益，從而降低噪聲系數，這已在上文中說明。對于過采樣，信號帶寬B低于fs/2。圖4給出了校正因數，因而噪聲系數的計算公式變為：

NF = 10log10F = PFS(dBm) + 174 dBm – SNR – 10 log10[fs/2B] – 10 log10 B.等式8

圖4：過采樣和處理增益對ADC噪聲系數的影響

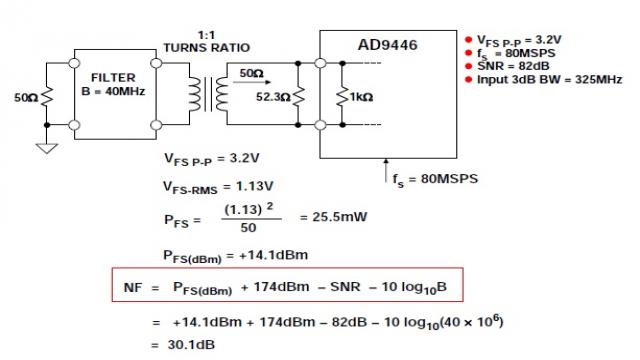
16位、80/100 MSPS ADC AD9446的計算示例

圖5顯示了16位、80/105 MSPS ADC AD9446的NF計算示例。一個52.3 ohm電阻與AD9446的1 k ohm輸入阻抗并聯，使得凈輸入阻抗等于50 ohm。ADC在奈奎斯特條件下工作，82 dB的SNR是利用上式8進行計算的基礎，得到噪聲系數為30.1 dB。

圖5：16位80/100 MSPS ADC AD9446

在奈奎斯特條件下工作的噪聲系數計算示例

級聯噪聲系數

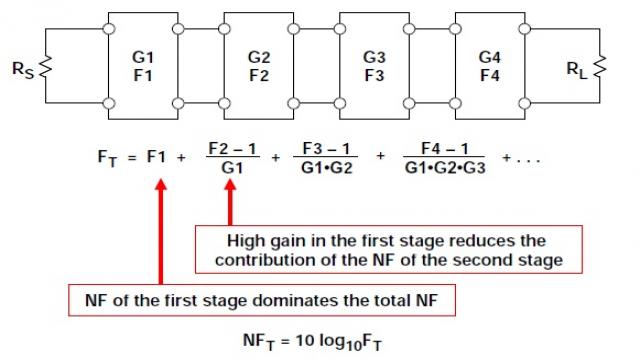
在一個典型接收機中，ADC之前至少有一個低噪聲放大器(LNA)和混頻級，它能提供足夠高的信號增益，從而將ADC對系統整體噪聲系數的影響降至最低。

這可以通過圖6來說明，其中顯示了如何利用Friis等式來計算級聯增益級的噪聲因數。注意，第一級的高增益降低了第二級噪聲因數的影響，因此第一級的噪聲因數在整體噪聲系數中占主導地位。

圖6：利用Friis等式計算級聯噪聲系數

圖7顯示了置于一個相對較高NF級(30 dB)之前的一個高增益(25 dB)低噪聲(NF = 4 dB)級的影響，第二級的噪聲系數是高性能ADC的典型噪聲系數。整體噪聲系數為7.53 dB，僅比第一級噪聲系數(4 dB)高3.53 dB。

圖7：雙級級聯網絡示例

結束語

應用噪聲系數概念來表征寬帶ADC時，必須特別小心，防止得出令人誤解的結果。試圖簡單地通過改變等式中的值來降低噪聲系數可能會適得其反，導致電路總噪聲提高。

例如，根據以上等式，NF隨著源電阻的增加而降低，但增加源電阻會提高電路噪聲。另一個例子與ADC的輸入帶寬B有關。根據等式，提高B會降低NF，但這顯然是相互矛盾的，因為提高ADC輸入帶寬實際上會提高有效輸入噪聲。在以上兩個例子中，電路總噪聲提高，但NF降低。NF降低的原因是源電阻或帶寬提高時，信號源噪聲占總噪聲中的較大部分。然而，總噪聲保持相對穩定，因為ADC引起的噪聲遠大于信號源噪聲。

因此，根據等式，NF降低，但實際電路噪聲提高。有鑒于此，當處理ADC時，必須小心處理NF。利用本文中的等式可以獲得有效的結果，但如果不全面理解其中涉及到的噪聲原理，這些等式可能會令人誤解。從孤立的角度看，即使是低噪聲ADC，其噪聲系數也會相對高于LNA或混頻器等其它RF器件。然而，在實際的系統應用中，ADC前方至少會放置一個低噪聲增益模塊，根據Friis等式(見圖7)，它會把ADC的總噪聲貢獻降至非常低的水平。

[聲明]文章版權歸原作者所有，內容為作者個人觀點，本站只提供參考并不構成任何投資及應用建議，轉載目的在于傳遞更多信息，并不代表本站贊同其觀點和對其真實性負責。如涉及作品內容、版權和其它問題，請在30日內與本網聯系，我們將在第一時間刪除內容！