惠州市嵐方實業有限公司
電話:400-6296-898
傳真:0752-2042189
地址:惠州市博羅縣羅陽鎮西北路8號
郵編:516100
FIR濾波器與IIR濾波器的區別和比較
IIR 濾波器和FIR 濾波器的比較和區別
1. 兩種濾波器都是數字濾波器。根據沖激響應的不同,數字濾波器分為有限沖激響應(FIR)濾波器和無限沖激響應(IIR)濾波器。對于FIR 濾波器,脈沖響應在有限時間內衰減為零,其輸出僅取決于當前和過去的輸入信號值。對于IIR濾波器來說,脈沖響應理論上應該是無限期的,它的輸出不僅取決于當前和過去輸入信號的值,還取決于過去信號的輸出值。
2. FIR:有限脈沖響應濾波器。有限意味著您的脈沖響應是有限的。與IIR相比,它具有線性相位和易于設計的優點。這也說明IIR濾波器具有非線性相位的缺點,不易設計。另一方面,IIR有一個FIR沒有的缺點,即要設計一個參數相同的濾波器,FIR需要比IIR更多的參數。這也說明應該增加DSP計算的次數。 DSP 需要更長的時間來計算,這會影響DSP 的實時性能。以下都是低通濾波器設計。 FIR設計:FIR濾波器的設計比較簡單,就是設計一個近似理想低通濾波器的數字濾波器。通常,這種理想的低通濾波器是頻域中的矩形窗口。根據傅里葉變換,我們可以知道這個函數是一個時域的采樣函數。通常這個函數的表達式是:sa(n)=sin(n)/n,但是這個采樣序列是無限的,計算機無法計算。因此,我們必須削減這個采樣函數。也就是加個窗函數。這就是傳說中的窗戶。即,為了將這個時域采樣序列乘以一個窗函數,這個無限的時域采樣序列被截斷為有限數量的序列值。但是,加窗后,采樣序列的頻域也有影響:此時的頻域不再是理想的矩形窗口,而是具有過渡帶和阻帶波動的低通濾波器。通常,根據所加窗函數的不同,對采樣信號進行加窗后,在頻域得到的低通濾波器消隱帶的衰減也不同。我們一般根據這個阻帶衰減選擇一個合適的窗函數。如矩形窗、漢寧窗、漢明窗、BLACKMAN窗、凱撒窗等。選擇特定的窗函數后,根據設計的濾波器的參數,計算出所需的窗函數階數和表達式。然后用這個窗函數乘以采樣序列,得到實際濾波器的脈沖響應。 IIR設計(雙線性變換法):IIR的設計理念是這樣的:根據要設計的濾波器的參數確定一個模擬濾波器的傳遞函數,然后根據這個傳遞函數,通過雙線性變換,或者脈沖的采用不變響應法設計數字濾波器。其設計較為復雜,其復雜性在于確定其模擬濾波器傳遞函數H(s)。我們可以讓軟件做到這一點。然后說一下你的具體實現步驟——你需要先確定你需要什么類型的濾波器,巴特沃斯型,切比雪夫型,或者其他類型的濾波器。
選擇模型后,可以根據設計參數和濾波器計算公式確定傳遞函數的階數和表達式。通常在這個過程中存在預失真問題(這只是雙線性變換方法中需要注意的問題,不變脈沖響應方法沒有這個問題)。確定H(S)后,可以通過雙線性變換得到數字域中的差分方程。 3.對于IIR和FIR的比較,有些書上有討論。我引用了陳懷臣的《數字信號處理教程-MATLAB的解釋與實現》:在性能上,IIR濾波器傳遞函數包括兩組可調因子,零和極點,唯一的極點限制在單位圓內。因此,可以使用較低的階數來獲得高選擇性,使用的存儲單元數量少,計算量小,效率高。但是這種高效率是以相位非線性為代價的。選擇性越好,相位非線性越嚴重。 FIR濾波器傳遞函數的極點固定在原點,不能移動,只能通過改變零點的位置來改變其性能。
因此,要實現高選擇性,必須使用更高的階數;對于相同的濾波器設計指標,FIR濾波器所需階數可以是IIR濾波器階數的510倍。因此成本較高,信號延遲也比較大;如果需要線性相位,IIR濾波器必須增加一個全通網絡進行相位校正,這也大大增加了濾波器的階數和復雜度。 FIR 濾波器可以具有嚴格的線性相位。從結構上看,IIR濾波器必須采用遞歸結構來配置極點,保證極點位于單位圓內。由于有限字長的影響,計算過程中系數會四舍五入,造成極移。這種情況有時會導致穩定性問題甚至寄生振蕩。相反,只要FIR濾波器采用非遞歸結構,理論上或在有限精度的實際運算中都不存在穩定性問題,因此引起的頻率特性誤差也很小。此外,FIR 濾波器可以使用快速傅立葉變換算法,并且在相同的順序下計算速度可以快得多。對高穩定的晶體振蕩器(高穩晶振)和高功率小型化腔體濾波器和介質濾波器都有成倍的配套需求,對其指標要求也很高;對應基站配套需求的時鐘模塊產品、授時守時模塊和時頻模塊對應的同比例的需求情況。
另外,還需要注意的是,IIR濾波器的設計雖然簡單,但主要用于設計低通、高通、帶通、帶阻等分段特性恒定的濾波器,往往與模擬濾波器模式。 FIR濾波器靈活得多,尤其容易適應一些特殊的應用,如構成數字微分器或希爾伯特變換器等,因此具有更大的適應性和廣泛的應用領域。從上面的簡單對比可以看出,IIR和FIR濾波器分別有所長,所以在實際應用中需要從多方面考慮選擇。從使用需求來看,IIR最適合于對相位要求不敏感的場合,比如語言交流,讓您可以充分發揮其性價比的特點;用于圖像信號處理、數據傳輸等系統。在波形中攜帶信息。線性相位要求更高。如果可能,最好使用FIR 濾波器。當然,在實際應用中可能需要考慮更多的因素。不管IIR和FIR,階數越高,信號延遲越長;同時,在IIR濾波器中,階數越高,對系數的精度要求越高;否則,極點移出單位圓時容易造成有限字長誤差。因此,在順序的選擇上要充分考慮。 IIR濾波器(切比雪夫濾波器) 濾波器比較(IIR和FIR,數字和模擬)第19、20、21章,主要講IIR濾波器和濾波器的比較IIR濾波器沒有使用卷積運算,而使用遞歸運算(遞歸),所以執行速度很快,但性能不一定比FIR濾波好。 IIR 的脈沖響應由衰減的指數信號組成。 IIR進出的重復率是: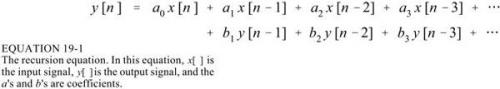
IIR的遞歸系數與其頻率響應的關系可以通過Z變換進行變換,這里不涉及。通過取不同的遞歸系數(下圖中的a和b),可以實現不同的濾波器:(9501.163.com)
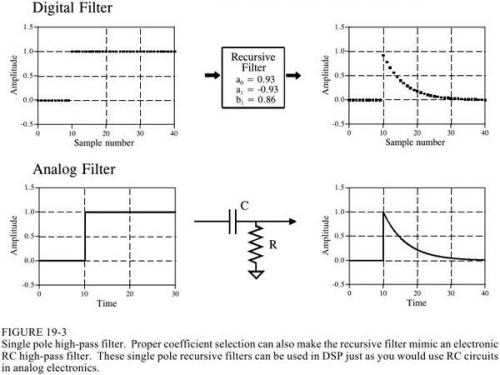
當然,這是最簡單的應用。遞歸系數的選取有一些細節和公式,這里不再贅述。 FIR 可以是線性相位,即脈沖響應是對稱的,而IIR 通常是非線性相位。這是因為FIR 在設計過程中決定了時域和頻率響應中的波形,而IIR 決定了設計中的遞歸系數,無法確定您的波形是什么樣的。 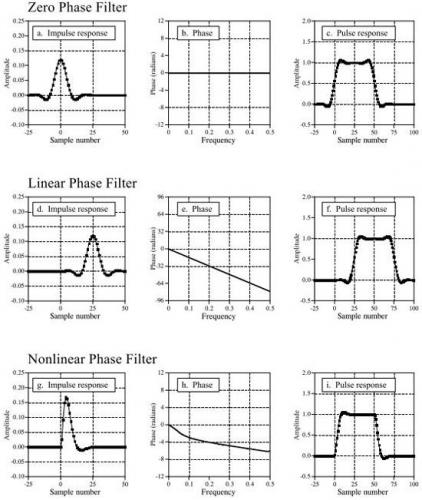
IIR實現線性相位,可以進行雙向操作,如下圖:(9504.163.com)
切比雪夫濾波器切比雪夫濾波器(Chebyshev)應用于頻域,其性能當然無法與同步窗函數濾波器相比,但速度非常快。 Chebyshev 響應是一種數學策略,通過允許頻率響應中的紋波來實現更快的衰減。隨著波紋度增加(壞),下降變得更劇烈(好)。 
了解極點:極點越多,性能越好。濾波器系數可參照下表確定。各種濾波器的比較1. 模擬與數字如果信號需要過濾,是否在模擬相位上過濾?還是數字化后過濾?下圖做一個對比,可以看出數字濾波器的性能與模擬濾波器難以實現,但速度較慢,模擬濾波器的幅度和頻率具有更高的動態范圍。 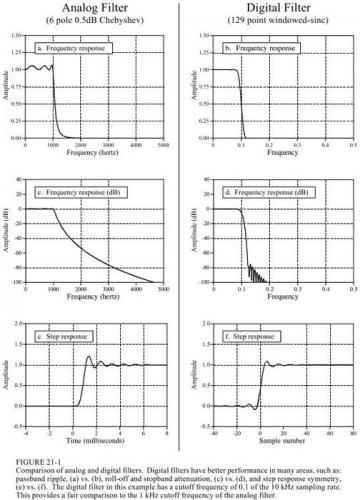
本例中模擬濾波的實現: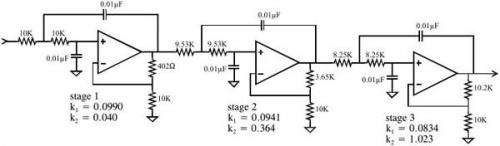
2、sinc vs Chebyshev窗函數對比下圖(9508.163.com)
sinc窗函數使用卷積進行運算,而Chebyshev使用遞歸方程。當然,卷積可以用fft卷積來完成,即先DFT,再進行頻域的4個算術運算,再進行逆DFT變換。這可以提高速度,但仍然不如遞歸方程快。另一方面,同步窗函數的濾波性能可以很好的發揮。 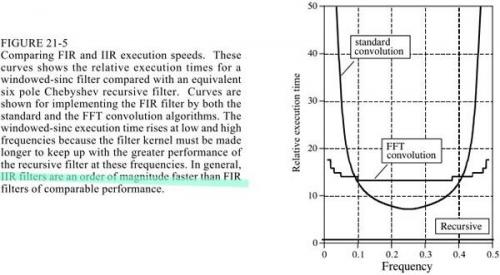
3. 移動平均對極點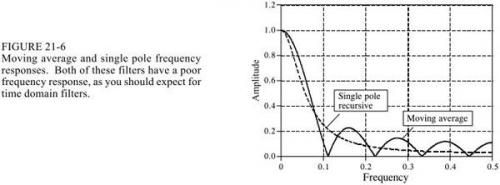
[聲明]文章版權歸原作者所有,內容為作者個人觀點,本站只提供參考并不構成任何投資及應用建議,轉載目的在于傳遞更多信息,并不代表本站贊同其觀點和對其真實性負責。如涉及作品內容、版權和其它問題,請在30日內與本網聯系,我們將在第一時間刪除內容!